|
|
||||
 |
Теория фокусов |
 |
||
|
Дата создания сайта: 24/02/2013 |
Карточные фокусы, фокусы и простые забавы | |||
|
|
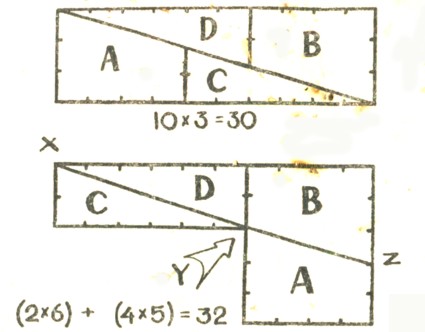
Фокусы с цифрами и числами Парадокс с площадью Покажите зрителям картонный лист с нанесенным на него прямоугольником площадью в 30 квадратных единиц и задайте вопрос, можно ли путем перестановки его частей получить фигуру большей площади - в 32 квадратные единицы. Как и в предыдущем парадоксе, здесь играют решающую роль только клетки, примыкающие к линии разреза. Остальные нужны только как оформление.
Рис 154 В этом парадоксе существуют два различных способа разрезания фигуры (рис. 154) на части. Можно начать с большего прямоугольника размером 3x10 единиц, аккуратно проводя в нем диагональ, тогда два меньших прямоугольника (рис. 154) будут на одну пятую единицы короче своих кажущихся размеров. Но можно также начать с фигуры, составленной из двух аккуратно начерченных меньших прямоугольников размером 2 х 4 и 4 х 5 единиц; тогда отрезки, соединяющие точку X с точкой Y и точку Y с точкой Z, не будут составлять прямую линию. И только потому, что образуемый ими тупой угол с вершиной в точке Y весьма близок к развернутому, ломаная линия XYZ кажется прямой линией. Поэтому фигура, составленная из частей малых прямоугольников, не будет в действительности прямоугольником, так как эти части-будут слегка перекрываться по диа-, гонали. Парадокс с шахматной доской, так же как и большая часть парадоксов этого плана, тоже могут быть представлены в двух вариантах. В одно^ из них парадокс получается за счет незначительного уменьшения или увеличения высоты (или ширины) фигур, в другом - за счет прироста или потери площади вдоль диагонали, вызываемых либо перекрыванием фигур, как в только что рассмотренном случае, либо появлением пустых мест. Меняя размеры фигур и наклон диагонали, этому парадоксу можно придать самое различное оформление. Можно добиться потери или прироста площади в 1 квадратную единицу или в 2, 3,4, 5 единиц и т. д. Конечно, чем дальше вы зайдете, тем легче будет обнаружить, куда деваются недостающие квадраты.
Читать далее про фокусы и фокусников...
|
|||
|
p.s. При копировании материалов и фотографий активная ссылка на сайт обязательна. |
||||
|
|
||||
|
|
||||